Mitigating Partial Observability in Sequential Decision Processes via the Lambda Discrepancy

Cameron Allen,^1* Aaron Kirtland,^2* Ruo Yu Tao,^2* Sam Lobel,² Daniel Scott,³ Nicholas Petrocelli,² Omer Gottesman,⁴ Ronald Parr,⁵ Michael L. Littman,² George Konidaris²

¹UC Berkeley, ²Brown University, ³Georgia Tech, ⁴Amazon, ⁵Duke University
*Equal Contribution

Paper Summary

RL in POMDPs is hard because you need memory. Remembering everything is expensive, and RNNs can only get you so far applied naively.

In this paper, we introduce a theory-backed loss function that greatly improves RNN performance!

The key insight is to use two value functions. In POMDPs, temporal difference (TD) and Monte Carlo (MC) value estimates can look very different. We call this mismatch the λ-discrepancy and we use it to detect partial observability.

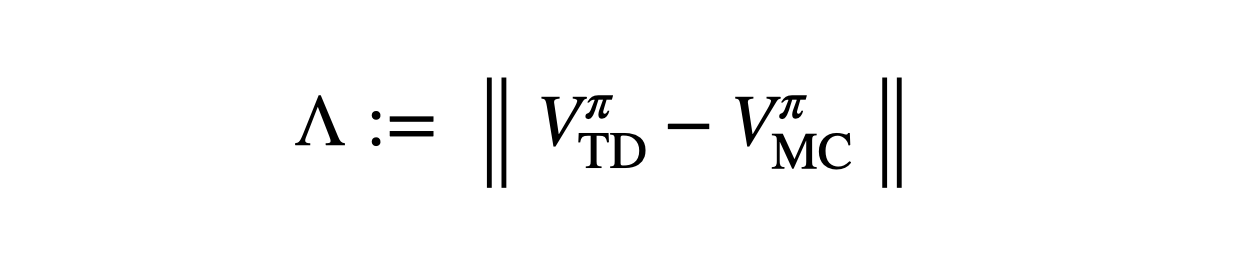
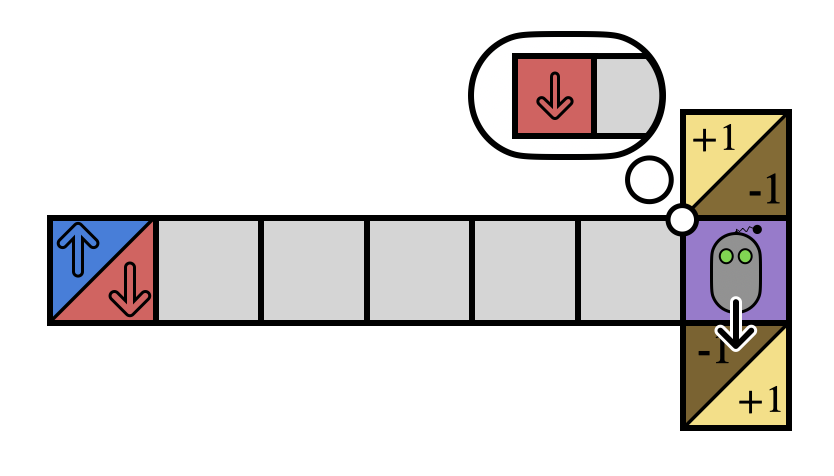
Here’s a quick example. Imagine you’re stuck inside this T-maze. If you can reach the +1, you win, and -1 you lose, but all you see is the current square. Without a map, how can you decide which way to go from the junction?

If you remember your whole history, you might notice the starting blue/red observation reveals the optimal action. But in general your history might be really long, so you only want to remember what you absolutely must.

How do we know if we need memory? This is where the value functions come in!

TD and MC have a λ-discrepancy in the T-maze, because TD uses bootstrapping (which makes an implicit Markov assumption), while MC computes a simple average.

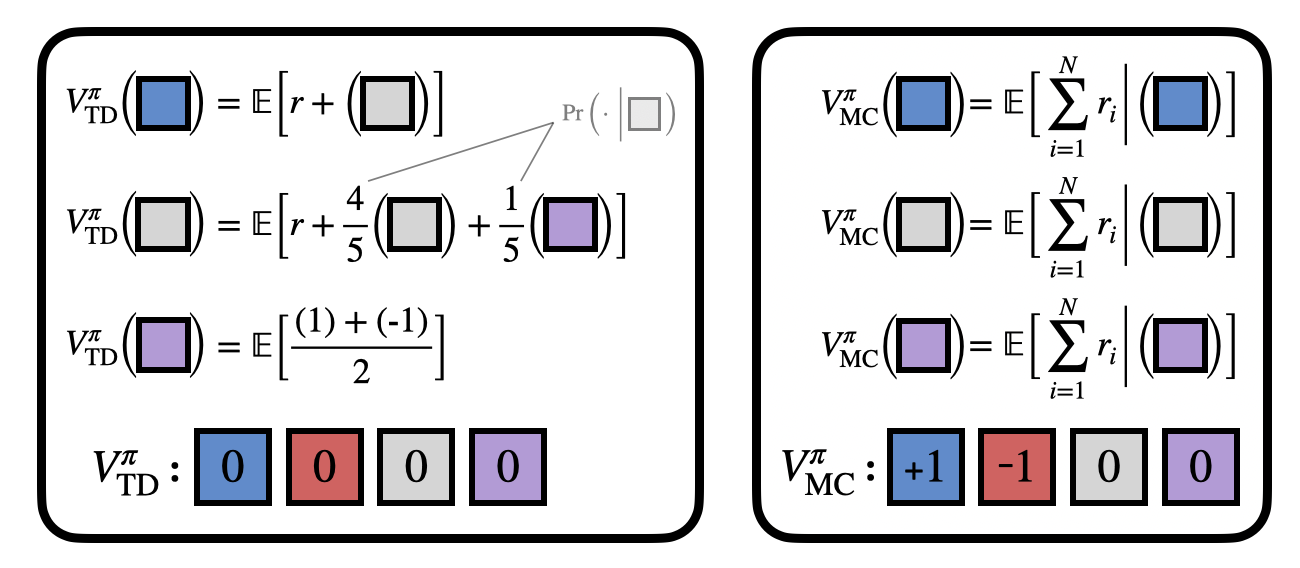
We can use the λ-discrepancy to detect partial observability. And it’s a very reliable signal!

We prove that if some policy has λ-discrepancy, then almost all policies will. Meanwhile, there is never a discrepancy for MDPs. (See the paper for the proofs.)

Okay, math is great, but how do we find a λ-discrepancy in practice? It’s actually super simple: just train two value functions and check the difference between them!

(Technically, we can compare TD(λ) for any two different λ values.)

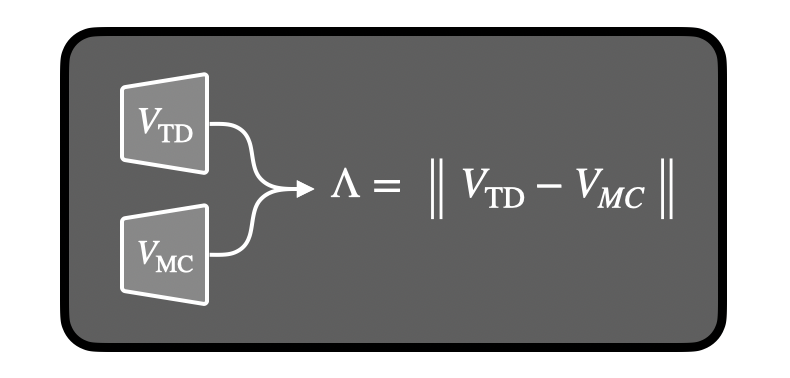
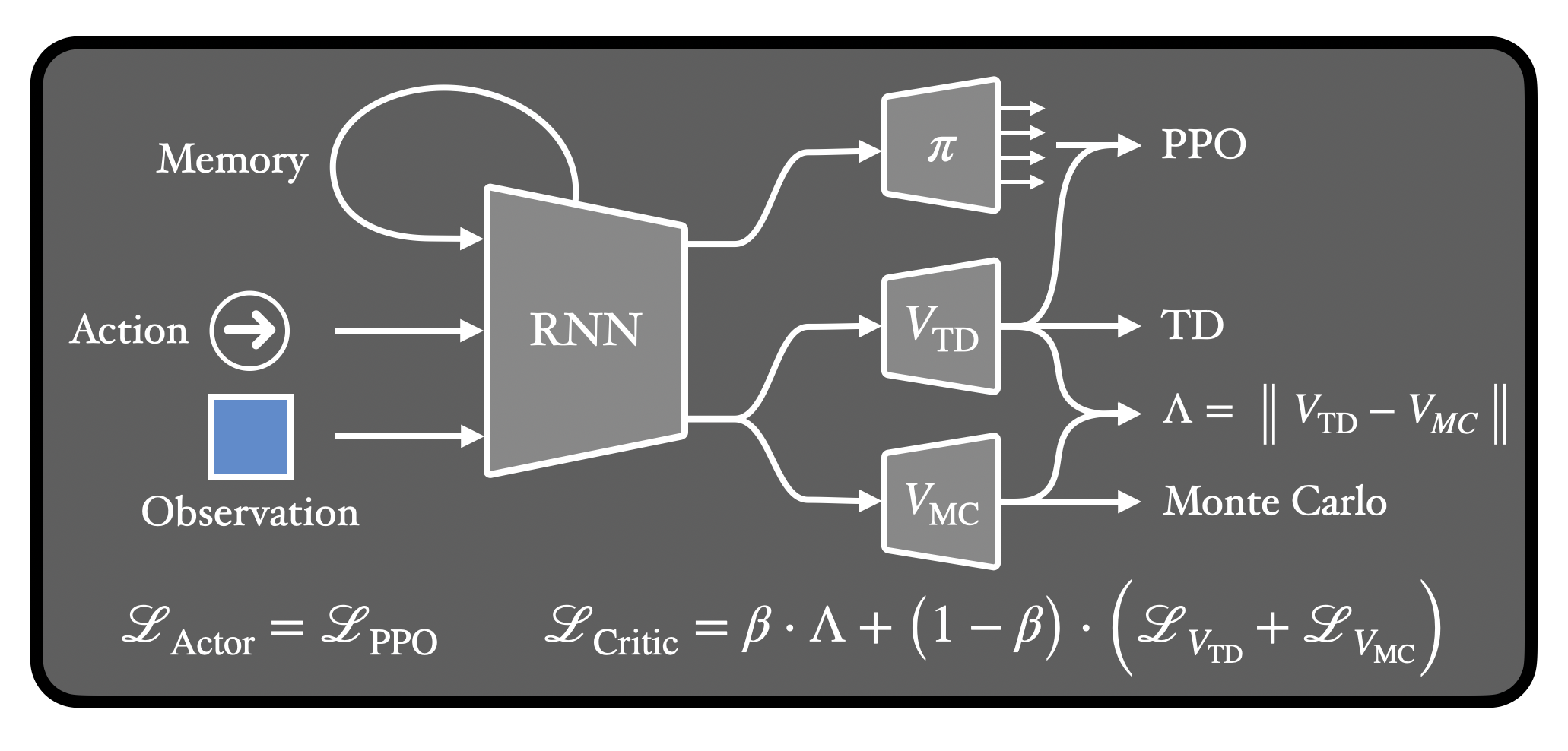
If we use an RNN, we can learn not just when we need memory, but also what state information to remember! All we do is minimize the λ-discrepancy while we train the value functions. And we can even train a policy at the same time!

We also trained a probe to reconstruct the PacMan dots from the agent’s memory. Guess which agent had an easier time with this… Yep! The λ-discrepancy agent knows where it has been, while the normal RNN agent basically has no idea.

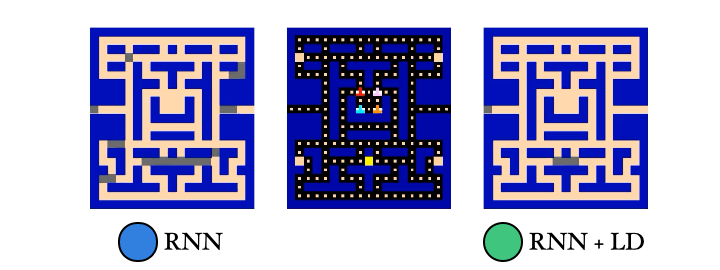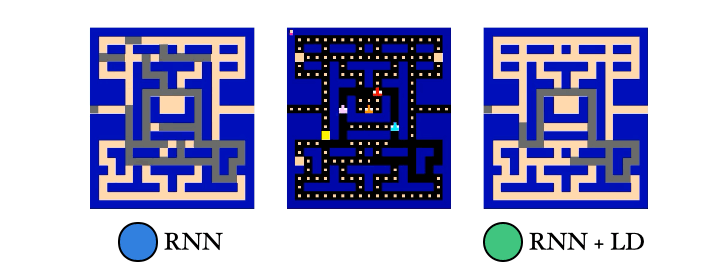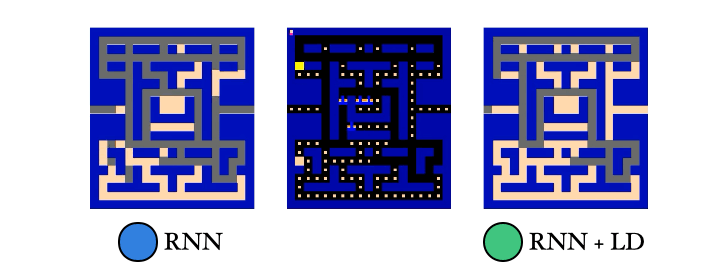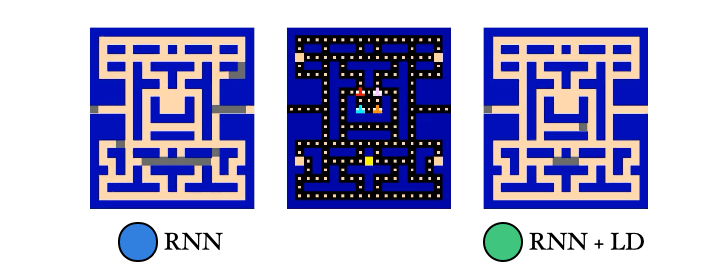
So to recap: (1) λ-discrepancy can detect partial observability; (2) reducing it leads to memories that support better policies; and (3) it significantly improves performance on challenging POMDPs.

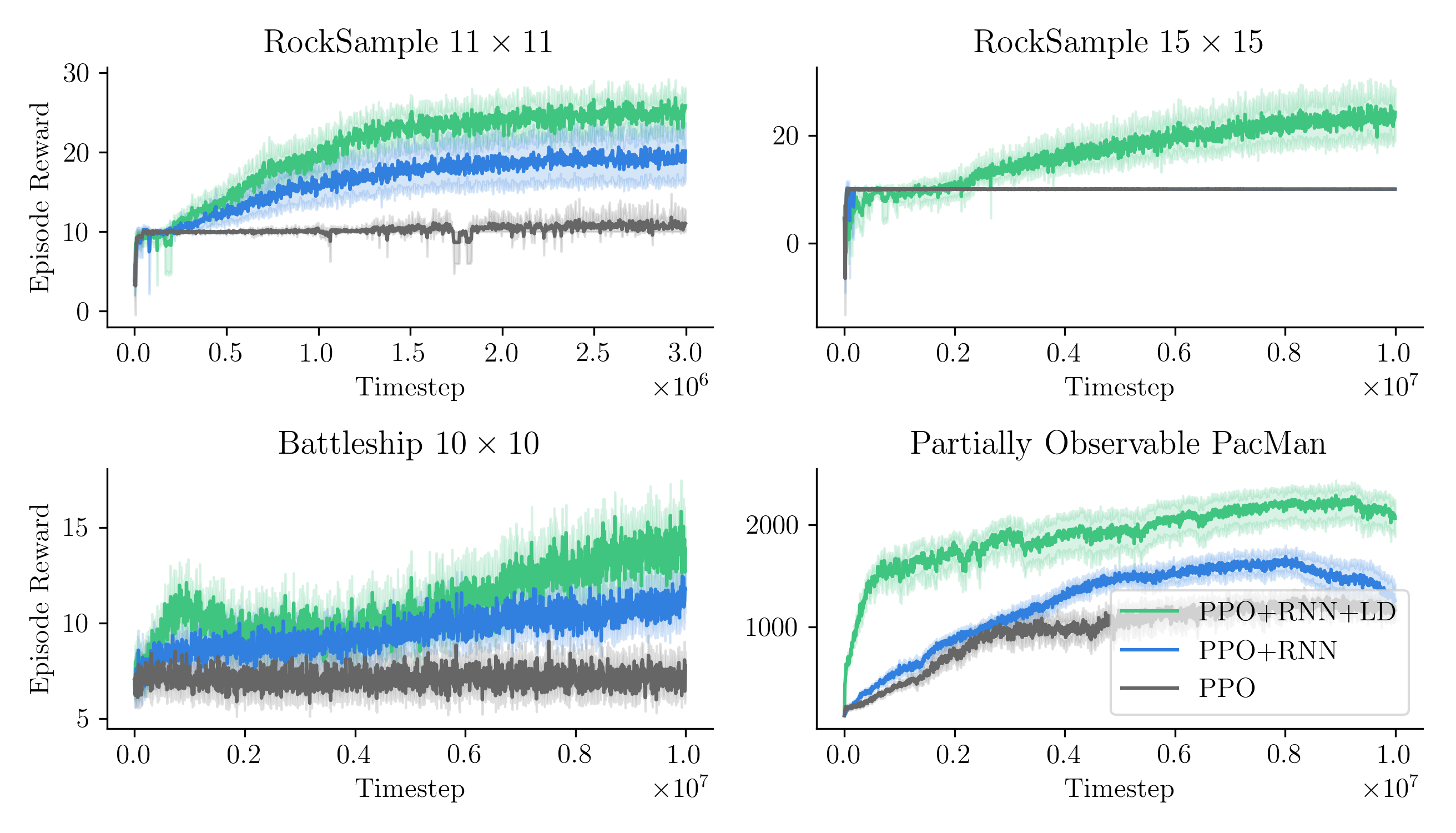
Check out the full paper to learn more!

Citation

@article{allenkirtlandtao2024lambdadiscrep,
  title   = {Mitigating Partial Observability in Sequential Decision Processes via the Lambda Discrepancy},
  author  = {Allen, Cameron and Kirtland, Aaron and Tao, Ruo Yu and Lobel, Sam and Scott, Daniel and Petrocelli, Nicholas and Gottesman, Omer and Parr, Ronald and Littman, Michael L. and Konidaris, George},
  journal = {arXiv},
  eid     = {2407.07333},
  year    = {2024}
}

Many thanks to Saket Tiwari, Anita de Mello Koch, Sam Musker, Brad Knox, Michael Dennis, Stuart Russell, and our colleagues at Brown University and UC Berkeley for their valuable advice and discussions towards completing this work. Additional thanks to our reviewers for comments on earlier drafts.

This work was generously supported under NSF grant 1955361 and CAREER grant 1844960 to George Konidaris, NSF fellowships to Aaron Kirtland and Sam Lobel, ONR grant N00014-22-1-2592, a gift from Open Philanthropy to the Center for Human-Compatible AI at Berkeley, and an AI2050 Senior Fellowship for Stuart Russell from the Schmidt Fund for Strategic Innovation.